| |
| |
The epicycloid is one of four cycloidal curves that are closely related. These are the
hypocycloid,hypotrochoid, epicycloid, and the epitrochoid. They are called roulette curves.
Roulette curves are traced on the locus of a point P, located somewhere on a circle of radius b, which rolls around a fixed circle of radius a.
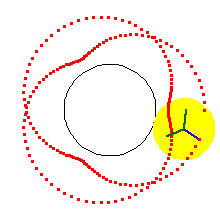
In the case of the cycloids, point P is located on the circumference of the circle B. In the trochoids, point P is located within or outside of the circle B.
In hypocycloids and hypotrochoids, the rolling circle B rolls on the inside of the fixed circle A. In epicycloids and epitrochoids, circle B rolls around the outside of circle A.
Period If a=1, then the period is b. if a=1 and b is irrational, then the curve is not periodic. |
|
| |
